題名:ゾンビウイルスの増殖率
報告者:トシ
具体的なゾンビウイルス自体は、そもそもまだ存在していない。そのため、少なくともアメリカのTV局により製作されているThe Walking Deadのような状況はそうそう訪れないであろう。しかしながら、未知のウイルスの爆発的な感染によるパンデミック(この記事も参照)な状況はいつなん時に起こり得ても不思議はない。その時、人は、映画のゾンビやTVのThe Walking Deadに見るフィクションとしてのゾンビ的な様相にはならなくとも、未知のウイルスの感染によって、ゾンビ的な症状を持たされる可能性も十分にあり得る。例えば、文献にも記載されているように、軍事目的による細菌兵器や生物兵器の研究により、ゾンビ的な症状がもたらされ1)、それによりパンデミックな世界になる可能性はもはや0ではない。すなわち、ゾンビウイルスの増殖率、などの知識があれば、備えあれば憂いなしとなり、パンデミックの早期に対策を講じることもできる。そこで、本記事では、具体的なゾンビウイルスの増殖率について検討したい。
ゾンビの増え方については、一般的には”ネズミ算”式に増えると言われている2)。”ネズミ算”とは和算の一つで、「ある期間に、ネズミがどれだけ増えるか」ということを計算する問題である3)。江戸時代前期の和算家である吉田光由が『塵劫記』に著した算術法であり3), 4)、その問題は、
正月に父ネズミと母ネズミが出て、子供を12匹(オスが6匹、メスを6匹)生みます。親と子と合わせて7つがい、14匹になります。二月になると、親も子供も1つがいにつき12匹ずつ生むので、全部で98匹になります。このように、月に1度ずつ、親、子、孫、ひ孫、とみな1つがいにつき12匹ずつ生むとき、翌年の正月には全部で何匹になるでしょう。
である5)。この”ネズミ算”は、先頃にこの記事にあったフィボナッチ数列と同じく、数列と見なせ、2×7n が答えとなる。ここで、nは月数である。ただし、ゾンビウイルスの場合は感染が早いため、月数でなく、日数と見なしてもよいかもしれない。そこで、この数列を基に、日数でのゾンビウイルスの感染者数をグラフ化すると、図のようになる。横軸が日数、縦軸が感染者数である。ゾンビウイルスの増殖率を、ウイルス感染者の数から考えると、5日以降はもはや逃げようにも逃げ切れそうにない。
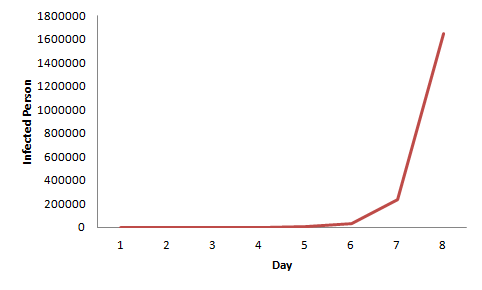
図 ”ネズミ算”により予想されるゾンビウイルスの感染者数
1) http://sonaeru.jp/hazard/infection/zombie/h-15/ (閲覧2016.11.28)
2) http://www.worldofthedead.org/archives/28812088.html (閲覧2016.11.28)
3) https://ja.wikipedia.org/wiki/ねずみ算 (閲覧2016.11.28)
4) https://ja.wikipedia.org/wiki/吉田光由 (閲覧2016.11.28)
5) 宮岡洋一: ネズミ算って知ってる? —等比数列と指数関数—. 藤岡おもしろ数学教室. 2011.
From ここから。© 2015 This is 地底たる謎の研究室 version。

